In questi appunti cerco di fissare le idee sui battimenti e sul problema generale dell'equabile
Rapporti di frequenza
Il nostro orecchio non fa somme o differenze di frequenze, ma moltiplicazioni e divisioni; cioè dati due suoni calcola il loro quoziente.
Così come l'ottava a salire è una frequenza raddoppiata, e l'ottava a scendere è una frequenza dimezzata, qualsiasi intervallo procede secondo questa regola.
Ciò significa che una quinta (es. DO-SOL) + un’altra quinta (SOL-RE) non è in realtà una somma ma una moltiplicazione.
Ad esempio, sapendo che il rapporto di quinta giusta si esprime matematicamente con 3/2, avremo:
DO 1/1; SOL 3/2; RE 3/2 x 3/2 ovvero (3/2)^2 = 9/4
Siccome tale RE è di una ottava più alto del DO di partenza per abbassarlo di ottava (sapendo che l’ottava è 2/1) devo fare la divisione, cioè
9/4:2/1= 9/8. Questo è il rapporto di seconda maggiore.
Es.: a partire da DO3=260Hz, avremo SOL3=260*(3/2)=390 Hz, RE4=390x(3/2)^2=585Hz; RE3=585/2=292.5
Il Cent
Vista la complessità di fare calcoli attraverso moltiplicazioni, potenze e divisioni, si è trovata un’unità di misura (Cent), definita come la centesima parte del semitono,
ovvero la 1200 parte dell’ottava.
Il Cent rappresenta in forma logaritmica un intervallo; sfruttando la proprietà dei logaritmi
log (a x b) = log a + log b
si ritrasformano le operazioni di prodotto in somme.
Vogliamo quindi misurare la "distanza" tra le frequenze F2 ed F1, cioè il rapporto F2/F1,
mediante il suo logaritmo (a meno di una costante): cioè D = log(F2/F1) x K.
Ma se vogliamo che l'unità di misura sia la centesima parte del semitono (il cent!), cioè la milleduecentesima parte dell'ottava (il rapporto 2/1), dobbiamo imporre:
Log2*K=1.200, da cui K=1200/Log2 = 1731.23404907
Trovata la costante, possiamo calcolare in cent tutti gli intervalli di cui conosciamo il rapporto di frequenze.
Ad esempio, per l'intervallo di quinta avremo: D = Log2(3/2) x 1731.23.... = 701,96 cent (702 cent).
Frequenza del suono e lunghezza della corda
La frequenza di un suono è inversamente proporzionale alla lunghezza della corda.
Ad esempio, se 1 è la lunghezza della corda della nota fondamentale, la corda della relativa quinta avrà lunghezza 2/3 (più corta),
e la nota avrà frequenza 3/2 (più alta); la corda della relativa terza maggiore avrà lunghezza 4/5 e frequenza 5/4, e così via.
La tavola seguente riporta i rapporti di frequenza dei singoli intervalli entro l'ottava,
e le frequenze dell'ottava A4-A5 per il temperamento naturale (rapporti puri) e per il temperamento equabile,
ed infine la differenza in cent tra i due temperamenti.
| Intervallo | Rapporto | Naturale | Equabile | Differenza Cent |
| I | 1:1 | 440 | 440 | 0 |
| IIm | 16:15 | 469.33 | 466.16 | -11.73 |
| IIM | 9:8 | 495 | 493.88 | -3.91 |
| IIIm | 6:5 | 528 | 523.25 | -15.64 |
| IIIM | 5:4 | 550 | 554.37 | 13.69 |
| IV | 4:3 | 586.67 | 587.33 | 1.96 |
| IV+ | 45:32 | 618.75 | 622.25 | 9.78 |
| V | 3:2 | 660 | 659.26 | -1.96 |
| VIm | 8:5 | 704 | 698.46 | -13.69 |
| VIM | 5:3 | 733.33 | 739.99 | 15.64 |
| VIIm | 9:5 | 792 | 783.99 | -17.6 |
| VIIM | 15:8 | 825 | 830.61 | 11.73 |
| VIII | 2:1 | 880 | 880 | 0 |
La IV+ è diversa dalla V dim, che sarebbe 64:45
|
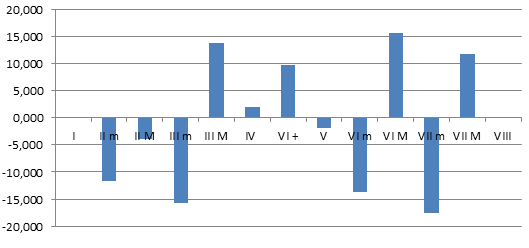
Il grafico rende visivamente evidente la differenza,
cioè quali intervalli devono essere crescenti e quali calanti
per ottenere un temperamento equabile a partire dal temperamento naturale.
Notare anche l'equilibrio attorno alla IV+, nota centrale.
|
Ottave per terze maggiori
Se divido un'ottava in tre terze maggiori nel rapporto perfetto 5/4,
ad esempio C-E,E-Ab,Ab-C, l'ultima terza sarà troppo calante per formare una ottava perfetta.
Infatti, se la corda che suona C è lunga 1, la prima terza (C-E) sarà 4/5,
la seconda terza (E-Ab) sarà 4/5*4/5=16/25, e l'ultima terza (Ab-C)
sarà 16/25*4/5=64/125 della lunghezza dell'intera corda.
Dato che l'ottava deve essere perfetta, la corda dovrebbe essere lunga 1/2 (la metà),
ma 64/125 non è la metà, perchè usando lo stesso numeratore, dovrebbe essere 64/128.
La differenza con la vera ottava C-C differirà di un rapporto 128/125.
La frazione 64/125 è un segmento più lungo di 64/128, per cui sarà calante.
Tutte le terze maggiori devono quindi essere accordate crescenti di 1/3 di questo rapporto per ottenere l'ottava pura.
Ottave per terze minori
Se divido l'ottava in quattro terze minori (rapporto 6/5) avrò:
C-Eb=5/6 della lunghezza; Eb-Gb=5/6*5/6=25/36;Gb-A=5/6*25/36=125/216; A-C=5/6*125/216=625/1296.
Divido il denominatore per 2 (1296/2=648) e lo metto al numeratore (648/1296=1/2)
per ricavare il rapporto per l'ottava pura (1/2).
La lunghezza della corda dell'ultima terza (625/1296)
è minore della lunghezza della corda per l'ottava pura (648/1296),
e quindi la corda più corta produrrà un suono crescente.
Il denominatore è lo stesso, quindi la differenza è 23/1296 della lunghezza dell'intera corda.
Il rapporto 648/625 esprime quanto l'ottava pura eccede rispetto a quattro terze minori.
Va da sé che per avere ottave pure, tutte le terze minori devono essere calanti di 1/4 di questo rapporto.
Ottave per quinte
Seguendo il circolo delle quinte si arriva da C ad E varie ottave sopra;
la E ottenuta sarà però troppo crescente per formare la terza maggiore C-E.
Quindi occorre fare quinte calanti, comunque le terze saranno crescenti.
Se le terze sono pure, le quinte saranno troppo calanti.
Dato che la quinta è più importante della terza, si preferisce calare le quinte lasciando però le terze crescenti.
Partendo da C1, rappresentata da una corda di lunghezza 1, la quinta sopra (G1)
sarà una corda lunga 2/3; la quinta successiva (G-D) sarà lunga 2/3*2/3, e così
via.
Per semplificare i calcoli, invece di moltiplicare 2/3*2/3=4/9,
e poi moltiplicare per due per rientrare dentro l'ottava, si può raddoppiare la
frazione 2/3 (2/3*2=4/3), ed usare 4/3 invece di 2/3 come moltiplicatore quando
è necessario raddoppiare il segmento per tenerlo entro l'ottava.
Iterando per tutto il circolo delle quinte si avrà:
| |
da |
|
a |
|
|
|
|
|
segmento di corda |
| 1. |
1C |
|
1G |
|
1 |
* |
2/3 |
= |
2/3 |
| 2. |
1G |
|
1D |
|
2/3 |
* |
4/3 |
= |
8/9 |
| 3. |
1D |
|
1A |
|
8/9 |
* |
2/3 |
= |
16/27 |
| 4. |
1A |
|
1E |
|
16/27 |
* |
4/3 |
= |
64/81 |
| 5. |
1E |
|
1B |
|
64/81 |
* |
2/3 |
= |
128/243 |
| 6. |
1B |
|
1F♯ |
|
128/243 |
* |
4/3 |
= |
512/729 |
| 7. |
1F♯ |
|
1C♯ |
|
512/729 |
* |
4/3 |
= |
2048/2187 |
| 8. |
1C♯ |
|
1G♯ |
|
2048/2187 |
* |
2/3 |
= |
4096/6561 |
| 9. |
1G♯ |
|
1D♯ |
|
4096/6561 |
* |
4/3 |
= |
16384/19683 |
| 10. |
1D♯ |
|
1A♯ |
|
16384/19683 |
* |
2/3 |
= |
32768/59049 |
| 11. |
1A♯ |
|
1F |
|
32768/59049 |
* |
4/3 |
= |
131072/177147 |
| 12. |
1F |
|
2C |
|
131072/177147 |
* |
2/3 |
= |
262144/531441 |
Il rapporto tra C e la sua ottava C2, procedendo per quinte, risulta quindi
262144/531441, che però non è uguale a 1/2, come richiesto per produrre
un'ottava pura.
Per essere 1/2, Usando lo stesso numeratore 262144, il denominatore dovrebbe essere 262144*2=524288.
Dato che 262144/531441 è minore di 262144/524288, l'ottava ottenuta con il circolo delle quinte sarà crescente rispetto alla ottava pura.
Il rapporto 531441/524288 è chiamato comma diatonico ed è uguale a 1/5 di un semitono (20 cent).
In conclusione, se le ottave devono essere perfette e desideriamo un
temperamento equabile, occorre dividere la differenza in 12 parti uguali, e distribuirla nelle 12 quinte del circolo.
Quindi si faranno le quinte calanti di 1/12 del comma diatonico (20cent/12 è uguale a circa 1.67 cent).
Temperamento equabile
Procedendo per quinte ci si trova con C4=C3*531441/262144=128*2.027Hz invece del puro C4=C3*2=256Hz,
cioè crescente di 0.027*2=0.54Hz; la differenza tra l'ottava pura 2/1 è di 0.54*2=1.08Hz, circa 1 battimento al secondo.
Se si vuole l'ottava pura (C4=C3*2), il comma diatonico (20 cent) sarà distribuito nei 12 intervalli
(20/12=1.67cent per intervallo).
Intervalli da abbassare: Quinta leggermente, minore terza e minore sesta considerevolmente;
Intervalli da alzare: Quarta leggermente, maggiore terza e maggiore sesta molto.
Battimenti
Se due corde producono lo stesso numero di vibrazioni al secondo, il suono sembrerà provenire da una unica corda.
Se una corda vibra a 100Hz e un'altra a 101Hz, ci sarà una porzione di tempo in cui le vibrazioni coincidono
ed un altro in cui saranno antagoniste.
In questo senso, "un battimento al secondo" vuol dire
che in un secondo ci sarà un periodo in cui il suono aumenta ed uno in cui diminuisce.
Due corde accordate all'ottava vibreranno in rapporto di 2/1. Se le due corde variano da questo rapporto di 1Hz, produrranno due battimenti.
Due corde che suonano un intervallo di quinta vibreranno in rapporto di 3/2; se variano questo rapporto di 1Hz, si produrranno tre battimenti al secondo.
Per le terze maggiori, con la variazione di 1Hz dal rapporto 5/4 si produrranno 4 battimenti al secondo.
Esempio pratico:
- Supposto C3=128Hz, l'esatta quinta dovrebbe essere G3=128/2*3=192Hz.
- Nell'equabile, la quinta deve essere contratta, cioè calante di poco meno di un battimento al secondo.
- Proviamo quindi cosa succede calando leggermente a G3=191.78Hz.
- Sottraendo il minore dal maggiore si ottiene 191.78-192=.22, cioè 22/100 di Hz.
- Moltiplicando per 3 questa differenza si ha .66, cioè circa 2/3 di un battimento al secondo.
Nell'ottava successiva avrò l'ottava pura C4=C3*2=256, e la sua quinta G4=G3*2=383.57,
con una differenza dalla quinta pura (G4=256/2*3=384Hz) di 0.43Hz in calare,
e quindi questa quinta dovrebbe avere 0.43*3=1.29 battimenti, circa 1 e 1/3.
Coprendo due ottave, l'ultima quinta del temperamento, da F4=341.72 a C5=512,
si dovrebbe avere un battimento calante di 1.74Hz, cioè circa 1 e 3/4 di battimento.